Масштабы планеты относительно человека настолько внушительны, что это не может не удивлять. Люди постоянно сравнивают массы и расстояния, причем еще и нашей планеты относительно других. Очень удобным оказывается тот факт, что Земля имеет шарообразную форму, что позволяет применять к ней классические и несложные математические формулы. С их помощью можно решать забавные и действительно интересные задачки. Это как помогает расширить кругозор, так и оттачивает математические навыки. Давайте попробуем решить пару таких задач. Их ответ поистине способен удивить.
💚 ПО ТЕМЕ: Янни или Лорл? Это невероятно, но люди слышат это слово по-разному. Что слышите Вы?
Задача о веревке с увеличенной длиной (земной шар и мышь)
Давайте представим, что земной шар имеет форму идеального шара и его перетянули по экватору веревкой. А теперь пофантазируем, что ее длину увеличили всего на один метр, что позволило немного отодвинуть веревку от поверхности Земли. Хватит ли полученного зазора, чтобы туда проскользнула мышь?
Решение будет очень простым. Учитывая, что R – радиус шара (нашей Земли), можно посчитать изначальную длину веревки
L=2πR
Можно найти радиус новой окружности, R0, зная, что новая длина окружности на метр больше предыдущей.
2πR0=2πR+1
Это приводит к следующему равенству:
R0=R+1/(2π)
Величина нашего зазора – это расстояние между радиусами:
R0-R=1/(2π)
Нетрудно подсчитать, что зазор составит 0,16 метра или 16 сантиметров. Хватит ли этого для мыши? Вполне! Но еще более удивительно то, что результат решения этой задачи не зависит от изначального радиуса шара. Другими словами, им могла бы быть не Земля, а Марс, Солнце или даже мяч. И каждый раз ответ будет одним и тем же. Можете для чистоты эксперимента обернуть мяч сантиметровой лентой, а потом добавить метр и оценить размеры новой окружности. Зазор и будет составлять те самые 16 сантиметров!
Доказательство на видео (теория):
Доказательство на видео (практика):
💚 ПО ТЕМЕ: 50 лучших оптических иллюзий.
Задача об оттянутой веревке
Эта известная задача похожа на предыдущую, ее ответ тоже может удивить. Давайте для упрощения представим, что наша Земля имеет форму идеального шара. Каким-то образом удалось обмотать ее веревкой точно по диаметру так, чтобы не было никакого зазора. А теперь зададимся вопросом. Если увеличить длину веревки всего на сантиметр и оттянуть ее в одном месте, то хватит ли этого пространства, чтобы туда прошел человек?
Для решения этой задачи примем, что радиус земли составляет 6371302 метра, тогда длина экватора составит 40 075 696 метров, согласно классической школьной формуле P=2πr. Решение задачи будет не таким уж и простым, это уровень старших классов или даже первого курса технического университета.
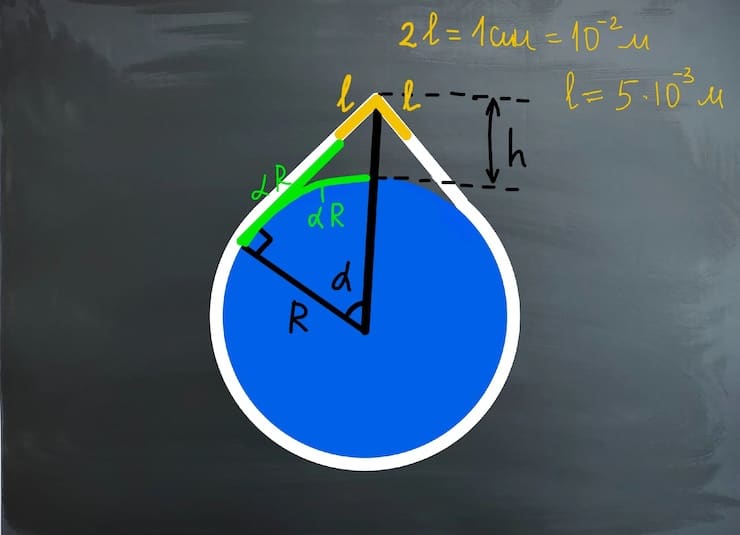
Попробуем представить то, о чем идет речь. Пускай земля будет неким синим кругом вокруг которого идет белая линия – та сама оттянутая веревка. Сверху это натяжение сформирует некий угол. Расстояние от его вершины до поверхности круга обозначим, как h. Задача требует узнать, достаточна ли будет эта высота, чтобы в нее прошел человек.
Конечно, придется прибегать к неким упрощениям. В масштабах планеты α – угол между новой вершиной и радиусом планеты столь мал, что можно считать sinα=α. Вспомним классическую школьную формулу косинуса двойного угла, используя наше упрощение:
cosα=1-2sin²(α/2)≈1-2(α/2)²=1-α²/2
Теперь давайте рассмотрим треугольник, который формируют радиус, расстояние от центра планеты до вершины отклонения веревки и сама веревка с точки отклонения поверхности до вершины. Этот треугольник прямоугольный, так что
cosα=R/(R+h)
Для дальнейшего упрощения к числителю прибавим и удалим h, а в левой же части приравняем cosα к 1-α²/2, учитывая малую величину угла. Получится следующее:
1-α²/2=(R+h-h)/(R+h)=1-h/(R+h)
Теперь из правой и левой части отнимем единицу и умножим на минус единицу для приведения к положительным значениям, получится:
α²/2=h/(R+h)
С учетом того, что h намного-намного меньше радиуса планеты, в тысячи, а то и в миллионы, то этой величиной в знаменателе можно пренебречь. Тогда формула примет такой вид:
α²≈2h/R (*)
Теперь самое время вспомнить формулу длины дуги S=α•R. На самом деле мы уже решили половину задачи.
Теперь давайте займемся этим треугольником. Тангенс угла α – это отношение противолежащего катета к прилежащему. Прилежащий равен увеличенному на величину h радиусу, а противолежащий формирует длина дуги и некий параметр l (очевидно, что 2l=1 см), то есть
tgα=(αR+l)/(R+h)≈α+l/R
Для малых углов можно разложить формулу с помощью ряда Тейлора до второго порядка:
tgα=α+α³/3
Сведя две последние формулы, получим:
α+l/R=α+α³/3
Сократив на α, получится следующее
l/R=α³/3
что приводит к
α³=3l/R
Возведем это равенство в квадрат, а помеченное звездочкой равенство в куб и приравняем их:
8h³/R³=9l²/R²
или
h³=9•l²•R/8
подставив значение длины и радиуса и извлекая корень третьей степени можно узнать точное значение высоты h
h³=9•0,005²•6371302/8=179 м³
h=5,63 метра
Так что теперь можно дать вполне однозначный ответ на вопрос – пройдет ли человек в этот зазор. Пяти метров для этого вполне достаточно. И этот ответ действительно удивляет. Не вдаваясь в вычисления кажется, что удлинение веревки всего лишь на сантиметр оставит маленькую щель, а зазор оказывается уж очень огромным!
🔥 Смотрите также: